之前簡單了解過 AVL 樹，知道概念但一直沒動手實踐過。Now
 
 AVL 樹是二叉搜索樹的一種。二叉搜索樹的規(guī)則就是：每個節(jié)點的 left child 都比自己小，right child 都比自己大。而 AVL 的在此之上又加了一個規(guī)則：每個節(jié)點的 left 深度與 right 深度只差<=1，這樣就能充分利用 二叉樹的結構，避免出現(xiàn)一個分支走到黑，導致搜索效率變低。如下圖：
                                             
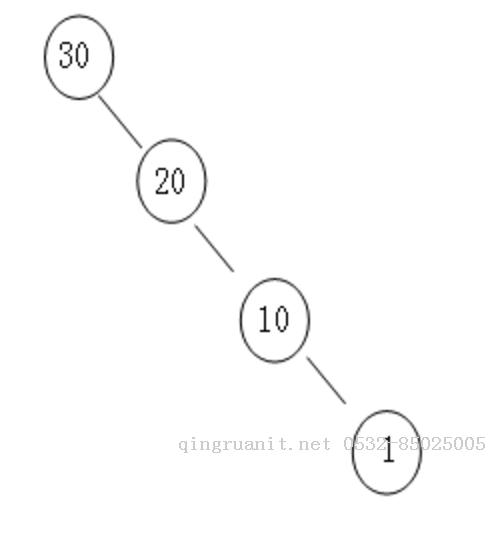
                                這種樹結構，搜索起來完全沒有體現(xiàn)出二叉搜索樹的優(yōu)勢
 
所以同樣多的元素，搜索樹的深度越低，就會越快的定位到搜索點。
 
AVL 樹為了保持樹的平衡，每次插入、刪除都會檢查 每個受影響的節(jié)點，深度差是否 <  1。最難的部分就是如果樹失衡，如何調(diào)整節(jié)點。插入的處理流程大致如下：
     給定一個 value，一路比較直到插入到某個位置。然后查找哪些節(jié)點因此而失衡，針對第一個失衡的節(jié)點進行旋轉(zhuǎn)。
 
下面是我從另一個博客上找來的圖（http://blog.csdn.net/gabriel1026/article/details/6311339），介紹了四種失衡的情況，以及調(diào)整方式：
注：圖中紅色的小塊 表示新插入的元素，A 點表示從插入點向上，發(fā)現(xiàn)的第一個失衡的點。
 
      AVL樹的旋轉(zhuǎn)一共有四種情形，注意所有旋轉(zhuǎn)情況都是圍繞著使得二叉樹不平衡的第一個節(jié)點展開的。

我想了解如何學習

姓名：
手機：
留言：